跳到主要内容
下载

第20卷增编1

第五届国际科学大会“植物遗传学、基因组学、生物信息学和生物技术”(PlantGen2019)文章精选

豇豆开花时间的动态气候模型

BMC植物生物学体积20.文章编号:202（2020）引用这篇文章

一个出版商校正本文发表于2021年1月15日

本文已被转载更新

摘要

背景

最近收集的物候资料约有300个豇豆属辐射动物(绿豆)是研究气候因素对植物生长影响的宝贵资源。

结果

我们建立了一个新的数学模型，描述了日最高和最低温度、降水、日照长度和太阳辐射对开花时间的动态控制。根据已有的实验数据，得到了模型参数。模型通过交叉验证验证，证明了花期等适应性性状的物候学不仅与当地环境因素有很强的预测关系，而且与植物的地理起源和基因型也有很强的预测关系。

结论

在局部环境因素中，最高温度似乎是决定模型对数据描述的忠实程度的最关键因素。应用该模型预测了台湾地区2020-2030年的开花时间。

背景

豆科植物中栽培的品种有绿豆(豇豆属辐射动物(l)Wilczek)，也被称为绿克)已成为亚洲和其他地区的重要作物之一，全球产量稳步增长(粮农组织2018年)。这种短期的豆类作物很容易作为轮作作物融入谷物生产系统，为接下来的作物增加土壤氮，并为农民提供额外收入。绿豆是一种有价值的蛋白质来源，含有大量的必需微量营养素叶酸和铁。除了绿豆的农艺价值外，由于其相对较小的基因组尺寸、较短的生命周期、自花授粉以及与其他重要的豆科作物密切的遗传关系，某些特征使其成为豆科植物中非常适合的模式生物。绿豆通常生产在边缘地区或炎热的季节，那里的非生物胁迫限制了它的生产力。绿豆黄花叶病(begomomvirus株)，由白蝇(烟)对产量和收成有重大影响[1］．

绿豆和相关物种的生物多样性收集可在不同的基因库中获得，例如:世界蔬菜中心(台湾)、国家植物遗传资源局(印度)、作物种质资源研究所(中国)、植物遗传资源保护单位(美国)、联邦科学和工业研究组织(澳大利亚)和植物遗传资源计划(巴基斯坦)。在n.i.v avilov全俄罗斯植物遗传资源研究所(俄罗斯)收集了1478份诉放射虫纲和230年的诉蒙戈［2，3.］．建立了各种核心集合，以改善育种中对绿豆生物多样性的获取[4］．

研究表明，高产绿豆品种应具有较大的叶面积、较高的总干量生产能力、各生长阶段的优良作物生长速度以及营养阶段较高的相对生长速度和净同化率，从而产生优良的产量成分[5］．对国际绿豆试验的分析表明，基因型-环境(G x E)之间存在很强的相互作用[6其中一些与生理性状有关，包括开花和成熟的时间。绿豆开花的时间受遗传和7]，以及环境管制[8］．绿豆种子产量的不一致性是由于其基因型对不同生长季节或生长条件的不同响应所致。一般来说，植物的生产力受管理的影响，此外还受气候、土壤类型、光周期响应和微环境等因素的影响。因此，基因型x环境相互作用的重要性在任何作物改良计划中都值得高度重视。有希望的基因型需要在数年的多环境试验中进行评估，以确定稳定和广泛适应的基因型[9］．

分子标记作为育种的组成部分，在世界范围内被广泛应用于所有主要作物。分子标记的开发和重要农艺性状标记-性状关联的建立加快了其他豆类育种的步伐[10]，但到目前为止，标记辅助选择作为绿豆育种计划的一部分的进展非常有限[11］．

在过去，人们曾多次努力开发与农艺性状相关的分子标记和连锁图谱，以进行绿豆的遗传改良，并最终进行品种培育，以提高绿豆的平均产量。最近公布的栽培绿豆参考基因组(V. radiata变种radiataVC1973A)和一种野生亲缘绿豆的额外从头测序(radiata变种)为绿豆遗传和基因组研究提供了一个框架，可扩展为全基因组关联和功能研究，以识别与特定农艺性状相关的基因[12，13］．野生绿豆的多样性基因库包含了宝贵的有益基因遗传资源，可能有助于扩大栽培绿豆的遗传多样性[3.，12］．

为了有效利用分子标记，整合基因型变异的作物物候模型可能是关键工具[14］．许多模拟模型已发展为其他栽培品种豇豆属还有绿豆。班巴拉族花生(豇豆属subterranea)，一种重要的油料种子作物，表型与花生相似，已用AquaCrop模型进行了检验[15］．虽然这些模拟的结果是初步的，但它们证实了这样一个观点，即班巴拉花生是一种潜在的未来作物，适合在边缘农业生产区种植。未来的研究应集中于作物改良，以提高班巴拉花生目前的产量[15］．APSIM模型可用于描述生长环境，进而可用于最小化对G x E相互作用的其他因素，包括管理物候以匹配目标生产环境。这种方法已用于高粱[16］．然而，APSIM模型需要进一步的改进和验证，以便其未来用于辅助育种项目[17］．

然而，在前基因组时代开发的模型最多将基因型影响视为一组与实际基因不对应的给定"遗传系数" [18］．结合遗传和气候数据来预测农艺性状的数学模型和工具将极大地造福育种者，因为它可以模拟任何给定的良好特征基因型在任何给定的良好特征环境中的表现[19，20.］．

自然选择塑造了种群的遗传变异，从而决定了当地的适应性[21］．基因组中适应的特征可以通过添加物起源地点的环境条件与snp之间的联系来揭示[22］．GWAS是一种很好的识别基因组区域和性状之间关联的方法，但它的设计通常需要受控的复制系的种植。这很快就会变成物流上的挑战和昂贵，特别是在多环境的路径上。作物模型可以通过考虑加入采样点的环境影响来补充GWAS方法。

在此基础上，我们对296个植物小核心种质的开花时间建立了新的动力学模型豇豆属辐射动物在不同年份和两个地点的四次田间试验中进行了表型分析。我们进一步利用该模型研究了基因型对环境因子的适应效应。最后，我们利用生成的每日天气预报2020-2030年的开花时间。

结果

对整个数据集的方差分析表明，不同产地之间的平均开花时间差异在标准值上无统计学意义F= 1.383,p= 0.125。因此，开花的时间不能用简单的与原产地国家的线性关系来解释，气候控制函数是可以找到的。

求模型参数(15)和(17的值，我们对每个模型执行了10次差分进化完全并行方法的优化运行λ= 1, 50100150200300500, 1000, 1500, 2000。每次运行使用不同的随机数生成器种子。

具有原产国信息的模型

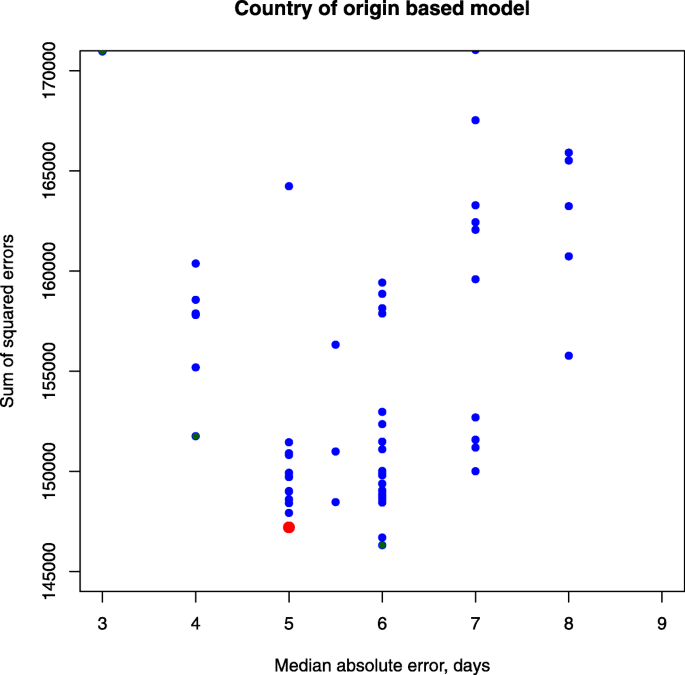
为了选择最好的模型进行进一步的研究，我们比较了模型和数据，并绘制了开花时间差异的平方和与该性状的中位数绝对差异(见图)。1)．最佳模型应该使这两个标准最小化，因此在图上对应的是最接近左下角原点点的值。

图1
图1

带有原产国信息的模型。每个模型都用一个点表示，最好的一个用大红点表示

全尺寸图像

所选模型由(定义1) - (6)．该模型预测开花时间的平均误差(均方根)为11.6天(λ=50)，花所需资源Y为40.27，系数阈值B最小值= 0.63。

$ ${}{{对齐}\ \开始δy(我,t) & = 0.83 f {0} + 4.45 \ \ cdot cdot f {1} + 0.13 f {2} + 9.57 \ \ cdot cdot f {3} \ \ & + 5.75 f{4} + \总和\ \ cdot limits_ {n = 0} ^ {4} \ Theta_ {n} f f {0} {n} \ \ & = \压裂{雨}{dl - 12.995} \ \ f{1} & = \离开((dl - 12.995) - \压裂{1}{dl - 12.995} \) \ cdot \压裂{1}{tmin - 0.109768} \ \ f{2} & = \离开(雨+ \压裂{1}{达峰时间- 29.9983}\右)f{3} \ \ & = \压裂{1}{雨- 20.582}\ \ f{4} & = \离开(\压裂{1}{srad - 2.60235} + \压裂{1}{tmin - 0.109768} \右)结束\ \ \{对齐}}$ $
(1）

在哪里Fn气候控制功能和Θn（2) - (6)描述附加的影响n对来自不同原产国的植物的作用。

$ ${}{{对齐}\ \开始Theta_ {0} & = \ \ & - 3.14988 \ cdot th - 3.06907 \ cdot - 3.7083 \ cdot af - 3.08391 \ cdot PK \ \ & - 3.96199 \ cdot ir - 3.00246 \ cdot PH值+ 0.641678 \ cdot br - 2.4291 \ cdot我们\ \ & - 3.10886 \ cdot au - 3.23838 \ cdot未知- 2.05882 \ cdot FR \ \ & \四\ cdot KR \ \ & + 0.635819 + 0.851436 \ cdot tr - 2.04774 \ cdot ng - 2.05237 \ cdot VN \ + \ 0.638283 \ cdot问\ \ & - 0.638868 \ cdot tw - 1.01931 \ cdot客\结束{对齐}}$ $
（2）
$$ {}{\begin{aligned} \Theta_{1} &=\\ &-3.17194\cdot TH+5.29528\cdot IN\\ &-9.33767\cdot AF+2.71034\cdot PK+8.32015\cdot IR \\ &-5.29786\cdot dr -9.11154\cdot BR-1.99994\cdot US+1.48757\cdot AU\\ &+7.79404\cdot US+ 2.83045\cdot FR+4.30076\cdot TR-9.17855\cdot NG\\ \ &-7.81195\cdot VN-8.69424\cdot IQ+2.64235\cdot NL+6.252\cdot TW\\ &-5.80664\cdot MX+3.24466\cdot KE \end{aligned}} $$
（3）
$ ${}{{对齐}\ \开始Theta_ {2} & = \ \ & + 4.26732 \ cdot th - 7.58479 \ cdot \ \ & - 8.24155 \ cdot af - 1.13634 \ cdot PK + 7.28225 \ cdot红外+ 9.38162 \ cdot PH值\ \ & + 5.94218 \ cdot br - 3.79285 \ cdot 1.25946 + 4.46692 \ cdot盟+ \ cdot未知\ \ & - 1.59303 \ cdot fr - 2.44954 \ cdot kr - 6.54573 \ cdot tr - 8.54903 \ cdot NG \ \ & + 9.20973 \ cdot VN + 2.88583 \ cdot IQ + 5.73987 \ cdot nl - 9.83768 \ cdot TW \ \ & + 4.34869结束\ cdot mx - 9.4759 \ cdot客\{对齐}}$ $
（4）
$$ {}{\begin{aligned} \Theta_{3} &= \\ &+9.29626\cdot IN+1.05261\cdot AF \\ &-1.82252\cdot PK+2.40813\cdot IR+5.6705\cdot h -5.5971\cdot BR \\ &+5.61499\cdot US+4.50366\cdot未知+1.04956\cdot FR\，+\，9.14113\cdot KR \\ &+7.68653\cdot TR-4.25743\cdot NG-6.3334\cdot VN-2.64341\cdot IQ \\ &-5.88418\cdot NL-2.45877\cdot TW+3.098\cdot KE \end{aligned}} $$
（5）
$ ${}{\开始{对齐}\ Theta_ {4 } &= \\ &+ 9.65241 \ cdot TH \ \ & + + 3.99315 \ 8.48755 \ cdot cdot af - 7.8144 \ cdot pk - 5.41556 \ cdot红外\ \ & - 8.92499 \ cdot ph - 2.06275 \ cdot BR + 6.47815 \ cdot 2.7679 + \ cdot盟\ \ & - 3.88322 \ cdot fr - 4.23494 \ cdot KR + 8.47326 \ cdot TR + 2.2374 \ cdot NG \ \ & + 4.6434 \ cdot VN + 7.29815 \ cdot智商- 5.41947 \ cdot nl - 9.54991 \ cdot TW \ \ & - 3.33689 \ cdot mx - 8.30075 \ cdot客\{对齐}}$ $
(6）

在公式(2) - (6)使用两个字母的国家代码代替指标变量d原产国:泰国(TH)，印度(IN)，阿富汗(AF)，巴基斯坦(PK)，伊朗(IR)，菲律宾(PH)，巴西(BR)，美国(US)，澳大利亚(AU)，法国(FR)，韩国(KR)，土耳其(TR)，越南(VN)，尼日利亚(NG)，伊拉克(IQ)，荷兰(NL)，台湾(TW)，墨西哥(MX)，肯尼亚(KE)。原产国和环境之间的相互作用占开花时间变异的12%。各原产国的实验数据与模型解的对比如图所示。2．虽然模型的平均误差较低，但模型解的范围小于数据中实际开花时间的范围。这可能是由于该模型描述了原产国对开花时间的影响，而没有考虑到归属于一个国家的品种之间这一性状的个体变异。

图2
图2

不同产地植物实际开花天数与预测开花天数的比较。每个点对应一种植物

全尺寸图像

通过对不考虑相关因素的模型和原始模型的预测误差进行比较，估计了气候因子对花期的影响。日照长度、降水、太阳辐射、最高温度和最低温度分别为2.3%、8.3%、5.4%、76.2%和7.8%。

为了比较国家间气候因素的影响，我们计算了每对国家影响平均值的Mann-Whitney-Wilcoxon检验(表2)。S3)。我们确定了118对来源国在气候因素影响上具有统计学上的显著差异，其中109对来源国的差异由最高温度造成。

具有基因型信息的模型

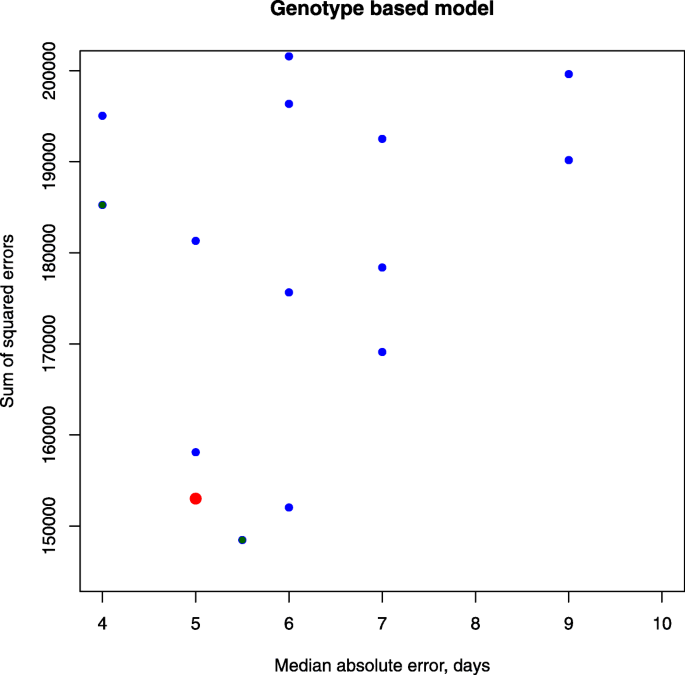
将模型与数据的开花时间平方和差值和中位数绝对差值同时最小化，选择为进一步研究的最佳模型。所选模型由λ=150，定义为(7) - (12)(图。3.)．开花时间、开花所需资源量的均方根误差和系数阈值分别为11.8天，Y= 56.55,B最小值分别为= 6.283。

$ ${}{{对齐}\ \开始δy(我,t) & f {0} + 7.18 = 6.65 \ cdot f {1} + 6.22 \ \ cdot cdot f {2} + 0.95 f {3} + 0.57 \ \ cdot cdot f {4} \ \ & + \ \ limits_总和{n = 0} ^ {4} \ Theta_ {n} f f {0} {n} \ \ & = \压裂{雨}{(雨- 18.6471)^ {2}}\ \ f{1} & = \压裂{1}{dl - 0.02289} \ \ f{2} & = \压裂{1}{tmin - 1.37714} \ \ f{3} & = \离开(\压裂{1}{dl - 0.02289} + \压裂{1}{达峰时间- 26.7143}\右)f{4} \ \ & = \压裂{1}{雨- 18.6471}\ \ \结束{对齐}}$ $
(7)
图3
图3

具有基因型信息的模型。每个点都是一个模型，最好的模型用大红点表示

全尺寸图像

在哪里Fn气候控制功能和Θn描述……的影响n-th功能在不同等位基因的植物上。在(8) - (12)而不是指示变量d从(17)使用SNP组的名称表示SNP编号和等位基因组合，其中“A”和“R”分别表示替代和参考等位基因。包含等位基因组合的植物Θn获得额外的功能影响Fn．

$$ {}{\begin{aligned} \Theta_{0} &= \\ &+7.4509\cdot snp4AR-8.16384\cdot snp6RR+7.69515\cdot snp7RR\\ &-7.99183\cdot snp9AR\\ \end{aligned}} $$
(8)
$$ {}{\begin{aligned} \Theta_{1} &= \\ &+9.22877\cdot snp1RR+9.28055\cdot snp3AR\\ &+7.15876\cdot snp5AA+7.92461\cdot snp5AR\\ &-9.27385\cdot snp6AR+7.54713\cdot snp7RR\\ &+ 6.7873\cdot snp7RR\\ &+6.79649\cdot snp7RR +7.17566\cdot snp9RR\\ &+8.43357\cdot snp10AA\\ \\ end{aligned}} $$
（9)
$${}{\begin{aligned} \Theta_{2} &= \\ &+7.37262\cdot snp1AA+9.13604\cdot snp1RR\\ &+9.12136\cdot snp2RR+9.98666\cdot snp3RR+9.22927\cdot snp5AA\\ &-9.23385\cdot snp5AR+9.71658\cdot snp7RR\\ \\ end{aligned}} $$
（10）
$${}{\begin{aligned} \Theta_{3} &= \\& +9.01623\cdot snp1AA\\ &+8.91822\cdot snp3AA+7.17114\cdot snp4AA\\ &\quad+8.60211\cdot snp4AA\\ &+7.46585\cdot snp5AA+7.2088\cdot snp5RR\\ &+7.62143\cdot snp6RR-6.30424\cdot snp7AA\\&\quad+8.76958\cdot snp7AR\\ & &+ 9.81541\cdot snp8RR+6.84716\cdot snp10AR-8.12269\cdot snp10RR\\ \\ \\ end{aligned}} $$
(11)
$${}{\begin{aligned} \Theta_{4} &=& \\ &-7.59475\cdot snp1AA-7.87434\cdot snp1AR+6.31816\cdot snp1RR\\ &-7.60708\cdot snp3AR+9.05006\cdot snp3RR+8.54655\cdot snp5RR\\ &+9.38654\cdot snp6RR+8.29729\cdot snp7AA-9.73811\cdot snp7aa -7.24539\cdot snp10AA\\ \\ \end{aligned}} $$
(12)

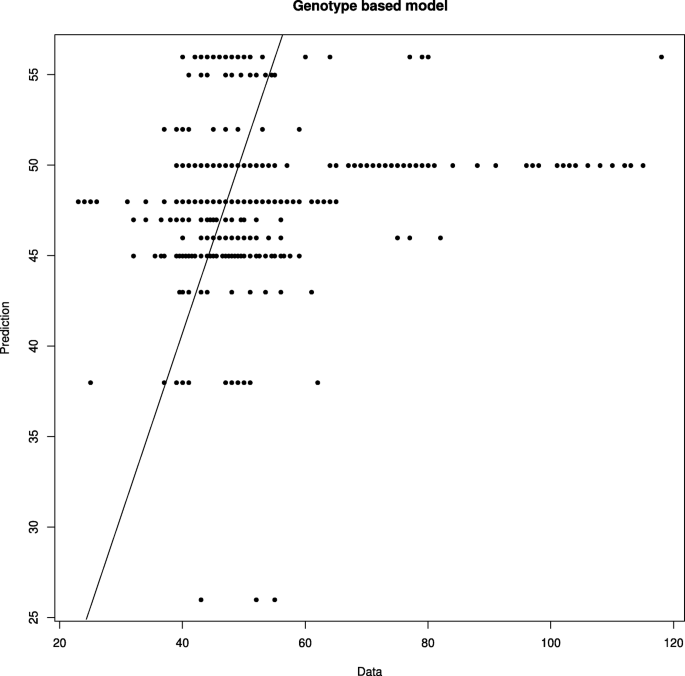
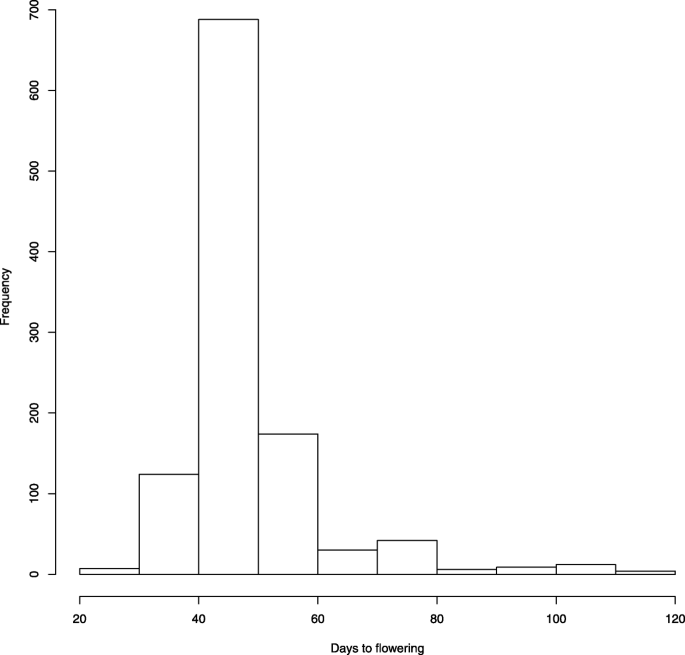
实验数据与模型解的对比如图所示。4．尽管模型准确预测了许多样品的开花时间，但57天以上的数值被低估了。这可能是由于这类样本对目标函数的影响有限，因为它们在数据集中的频率很低(见图中的直方图)。5)．

图4
图4

模型预测的开花天数与基因型信息和数据的比较。每个点对应一种植物。直线对应一个理想情况，即当预测等于数据

全尺寸图像
图5
图5

可用数据集中开花时间的直方图

全尺寸图像

利用整个数据集的75%的样本进行训练，用25%的样本进行测试，通过4倍交叉验证测试进一步验证模型对独立数据集的泛化能力。训练集与测试集均方根差异均数比较的t检验差异无统计学意义(P= 0.17 > 0.05)。将开花时间均方根误差与Mann-Whitney-Wilcoxon检验进行比较，再次发现训练与测试的差异无统计学意义，分别为28.44天和30.41天。

基因型-环境相互作用占该模型误差的19%，根据(20.)．通过对不考虑相关因素的模型和原始模型的预测误差进行比较，估计了气候因子对花期的影响。结果表明，日照长度对降水的影响为20%，降水量为2.5%，最高气温和最低气温分别为63.5%和14%。

为了了解气候因素对不同等位基因组合的花期的影响，采用Mann-Whitney-Wilcoxon检验比较了组合对各因子影响的平均值。我们确定了309对对气候因素的不同响应(见表。S4)。例如，带有SNP1AA和SNP1AR或SNP1AA和SNP1RR等位基因组合的亲本对日照长度和最低温度的反应不同，而带有SNP2AA和SNP2AR、SNP3AA和SNP3AR、SNP4AA和SNP4AR、SNP7AA和SNP7AR、SNP8AA和SNP8AR、SNP9AA和SNP9AR等位基因组合的亲本对所有因子的反应都不同。

预测

以上对整个数据集进行的交叉验证表明，具有基因型信息的模型(17)具有良好的预测能力。然而，要预测进入植物开花的时间，需要确信所开发的模型可以推广到未来的数据集。由于可供我们使用的数据集数量有限，我们将2018年的数据集作为“前瞻性”数据集，同时在其余数据集上构建和验证模型。1984年、1985年和2016年的数据集被分为验证(105条记录)和核心数据集，如材料和方法中所述。保存了2018年(292条记录)的数据，用于前瞻性预测。然后对核心数据集执行4次交叉验证，结果是100次拟合运行。训练集与测试集均方根差异均数比较的t检验差异无统计学意义(P=0.77>0.05)。Mann-Whitney-Wilcoxon检验也显示训练与测试之间无统计学差异，分别为26.20天和27.08天。

选择最佳模型，使模型与数据的差平方和和和中位数绝对差最小。预测开花时间的均方根误差为5.8天(见附加文件)1)．然后应用该模型预测了2018年验证数据集和“预期”数据集的开花时间。我们发现这些数据集的均方根误差分别为5.82天和5.34天。验证数据集和“前瞻性”数据集的数据和模型解之间开花天数的中位数绝对差异也很小，分别为3天和4天。模型解对试验、验证和“前瞻性”数据集具有较高的准确性，证明了其良好的预测能力和预测开花时间的适用性。

模型(7) - (12)用于预测整个数据集(293份资料)2020-2030年和台湾地区未来年份的开花时间。MarkSim软件为四个rcp生成了三个每日天气的副本。

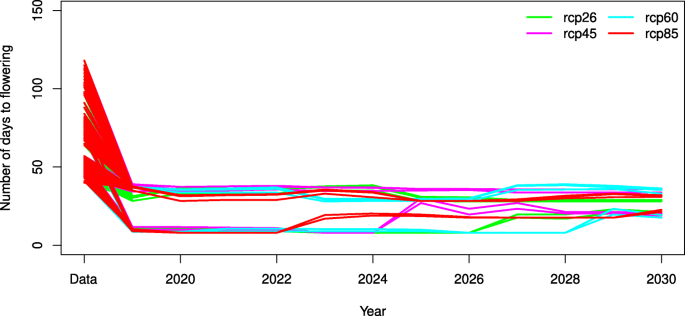
我们发现，与现有数据相比，在所有四种气候变化情景下，所有资源的开花时间都减少了，但不同的资源组遵循不同的轨迹，可以合并为两个集群，开花时间分别为>25天和<25天(图1)。6)．第一个聚类的轨迹波动幅度较小，各类群的开花时间在模拟周期内没有显著增加。rcp85、rcp60、rcp45和rcp26的开花时间分别为2023年、2025年、2029年和2027年。rcp45的开花时间从2025年开始慢慢减少。

图6
图6

对293份材料的花期预测平均超过3个重复的日天气

全尺寸图像

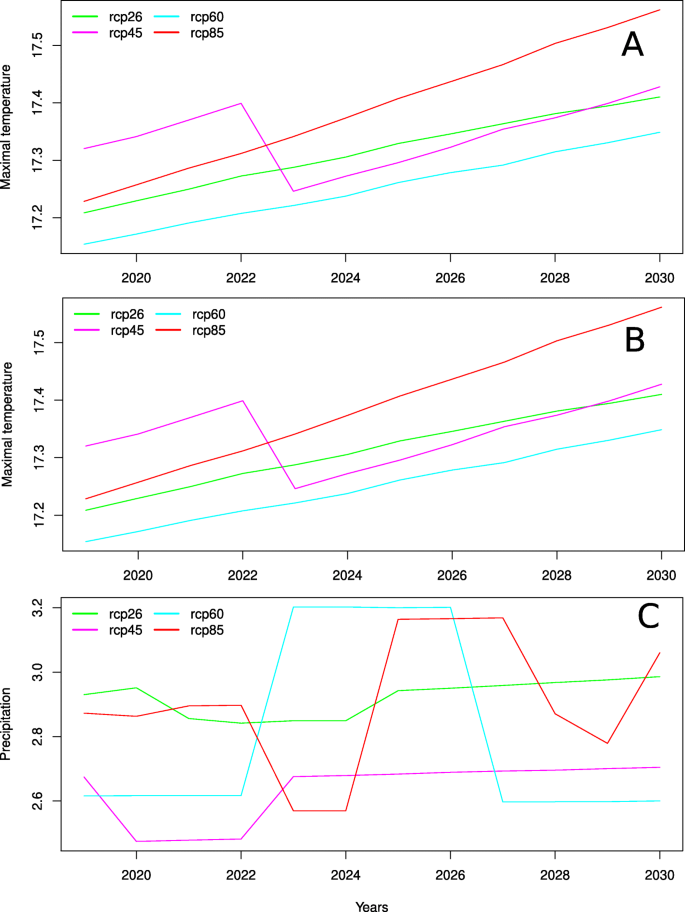
从图中可以明显看出。7A,b除rcp45的开花时间在2023年下降外，所有品种的开花时间都是由温度的普遍影响造成的，而温度的影响正在稳步增加。开花时间的波动可以用降水的波动来解释。7c).不同的轨迹显示了不同的群体对气候变化的响应差异，这是由气候因素，特别是最高温度对具有不同等位基因组合的群体的开花时间的不同影响所决定的。此结论由公式(7) - (12)，在相同的播种日期和气候条件下，只有不同等位基因组合的亲本才能获得不同的开花时间。第一个类群中的植物对气候变化的响应几乎是单调的，其开花时间值与模型期相近，而2022年后形成第二个类群的植物则增加了开花时间，并向第一个类群靠拢。

图7
图7

最小的(一个)和maximum (b)气温和降水(c)，并在3次试验和从播种到年底期间的平均值

全尺寸图像

讨论

在许多热带和亚热带地区，绿豆(豇豆属辐射动物)现在是一种重要的豆科植物，因为它的存贮时间短，种子可以快速煮熟，而且能够适应温暖的季节进行轮作。越来越多的绿豆也在温带地区生产，如中亚、澳大利亚和美国南部大平原。在这些环境中，开花时间是一个关键的特征，因为许多轮作伙伴，如小麦，在冬天生长，通常在春天收获相对较晚，绿豆生产转移到条件，在寒冷天气开始前，短时间的结实期尤为关键。

本文建立了一个新的数学模型，描述了日最高和最低温度、降水、日照长度和太阳辐射对绿豆开花时间的动态控制。在模型开发中，采用了语法进化和差分进化完全并行方法相结合的解决方案，其中预测因子(气候因素、来源国和基因型)和表型(开花时间)之间依赖关系的解析形式通过随机优化技术自动推断。这使得快速检查数据的不同适合度并选择最佳的一个成为可能。模型是对来自20个不同国家、在4个不同环境中表型的293个绿豆品种数据集的参数化。GWAS分析了最近进行的数据(Sokolkova等人，在准备中)确定了10个负责开花时间的多态位点。

几项研究表明，适应性性状的物候学，如开花时间，不仅可以通过当地环境因素，而且可以通过植物的地理起源强有力地预测[39，40(Sokolkova等人，提交)。此外，由于对特定环境的适应是在基因组中绘制的蓝图[41，42]，不同的基因型应以不同的方式对当地环境作出反应。我们的工作证实并进一步发展了这些想法。我们建立了两类模型，根据原产国或基因型考虑气候因素对开花时间的影响，发现开花时间的变化分别有12%和19%是由气候因素与这些变量的相互作用造成的。与以往测量表型对所有环境因素的综合敏感性的方法相反，我们的方法使确定特定的环境条件如何影响该性状成为可能。最高温度似乎是决定模型如何忠实描述数据的最关键因素。

用比较的方法进一步证实了原产国和基因型对植物物候的影响。我们发现，在不同等位基因组合的材料中，气候因素对开花时间的影响是不同的。例如，带有SNP1AA和SNP1AR或SNP1AA和SNP1RR等位基因组合的亲本对日照长度和最低温度的反应不同，而带有SNP2AA和SNP2AR、SNP3AA和SNP3AR、SNP4AA和SNP4AR、SNP7AA和SNP7AR、SNP8AA和SNP8AR、SNP9AA和SNP9AR等位基因组合的亲本对所有因子的反应都不同。当考虑到气候因素与原产国的相互作用时，我们也得出了类似的结论:我们确定了118对气候因素影响之间存在统计学上显著差异的国家对，其中109对的差异由最高温度造成。

对重要农艺性状的预测对于为作物生长的最佳管理和国家粮食安全及时提供信息至关重要。本研究利用该模型预测了台湾地区2020-2030年的开花时间。然而，要使预测可靠，就需要证明模型一般可以推广到独立的数据集，特别是未来的数据集。对整个数据集进行交叉验证表明，我们的模型具有良好的预测能力:在训练数据集和测试数据集上的预测精度差异在统计学上不显著。由于可供我们使用的数据集数量有限，我们将2018年的数据集作为“前瞻性”数据集，同时在其他数据集上构建和验证模型。再次，我们能够表明，模型预测误差在这个前瞻性数据集是小的。结果表明，该模型具有较好的预测能力，可用于预测花期。

为了预测开花时间，考虑了四种气候变化情景rcp26、rcp45、rcp60和rcp85，由于未来人为温室气体排放的可能变化，它们对2100年的地球辐射平衡有不同的预测[38］．我们发现，虽然所有材料的开花时间都在缩短，但不同的材料组对相同的气候变化情景的反应不同，这些差异是由气候因素和最高温度对具有不同等位基因组合的材料的开花时间的不同影响所决定的。例如，有一组品种的开花时间从2020 - 2022年开始减少，然后在不同rcp的不同年份增加。预测的气温和降水趋势表明，花期的波动是由降水波动驱动的，而花期的整体减少是由于气候变暖。

结论

考虑了受产地或基因型影响的最大和最小温度、降水、日长和太阳辐射日值对绿豆开花时间的动态控制的两类模型。结果表明，花期等适应性性状的物候变化不仅与当地环境因素有密切关系，而且与植物的地理起源和基因型也有密切关系。在局部环境因素中，最高温度似乎是决定模型对数据描述的忠实程度的最关键因素。

将该模型与基因型信息进行交叉验证，并应用于预测2020-2030年台湾地区品种的开花时间。由于不同等位基因组合的材料对开花时间的影响不同，它们对相同气候变化情景的响应也不同。结果表明，花期的整体缩短是由气温升高引起的，而花期的波动则是由降水的波动引起的。

方法

植物材料

从WorldVeg的7,965个绿豆条目中建立了一个包含296个基因型的绿豆迷你核心集合，如[4］．简单地说，整个收集基于地理来源进行分层，然后基于8个形态描述符聚类。从每个集群中随机选择20%的条目，产生1481个条目的核心集合。用25个微卫星标记对核心集进行基因分型，选择代表所有检测到的122个等位基因的最小集，得到296个小核心集。

迷你核心系列包括来自:泰国(TH)，印度(IN)，阿富汗(AF)，巴基斯坦(PK)，伊朗(IR)，菲律宾(PH)，巴西(BR)，美国(US)，澳大利亚(AU)，法国(FR)，韩国(KR)，土耳其(TR)，越南(VN)，尼日利亚(NG)，伊拉克(IQ)，荷兰(NL)，台湾(TW)，墨西哥(MX)，肯尼亚(KE)。表S1显示了每个区域的样本数量。

可用的数据集是在实地实验中组成的:

  • 1984年:播种于28/08/1984;24/10/1984收获。地理坐标:n23∘6 ' 50" e 120∘17“55”,

  • 1985年:17/09/1985播种;03/10/1985收获。地理坐标:n23∘6 ' 50" e 120∘17“55”,

  • 2016年:2016年6月16日播种，8月22日至9月中旬收获。地理坐标:n17∘30 ' 28" e 78∘16“10”,

  • 2018年:2018年9月21日播种，2018年12月24-28日收获。地理坐标:n23∘6 ' 50" e 120∘17“55”。

图中给出了数据集中开花时间的直方图。5．

GWAS

我们使用了最近一项与开花时间相关的GWAS分析中发现的10个snp (Sokolkova等人，在综述中)。简而言之，基于5041个SNPs，利用FaST-LMM工具集(因子光谱变换线性混合模型)实现的单位点线性混合模型，在293个系中识别出snp [23］．LMM模型采用前10个PCA轴得分作为协变量。我们使用了错误的发现率(FDR) [24，以确定显著性状相关位点。在GWAS分析中，发现了10个与开花时间相关的snp。这些snp的坐标、等位基因组合和附加信息显示在Tab中。S2。

气候数据

田间试验期间每天的气候条件数据取自公共站点https://rp5.ru/Weather_in_the_world(网站提供172,500个地点的天气预报，以及气象站报告的观测数据)和NASA [25(这些数据来自NASA兰利研究中心(LaRC) POWER项目，由NASA地球科学/应用科学项目资助):

  1. 1.

    戴斯。莱纳姆:或D是一天的长度,

  2. 2.

    tmin或Tn是最低温度，

  3. 3.

    达峰时间或Tx是最高温度，

  4. 4.

    雨或P降水,

  5. 5.

    srad或年代是太阳辐射。

仿真模型

在[18该框架是为结合天气和SNP数据而开发的。我们通过引入非线性和自动函数选择进一步增强了该方法。仿真模型描述了植物开花的准备情况y（我，t指植物我每天都在增加t从播种(t=0)到实际开花(t＝T我)．为了增加它的准备，植物积累资源和每日增量Δy（我，t)取决于白天的环境t和工厂环境交互。

$ $ \{对齐}开始(我,t) & = y(我,t - 1) + H(\δy (i、t)) \δy(我,t) \ \ y(我,0)& y = 0 \四(我T_{我})识别\组y \四y(我T_{我}识别1)< y \{对齐}$ $
（13）

在哪里Y一株植物开花需要积累的资源量是多少H()是一个Heaviside函数。

文献中已经提出了几种依赖形式。在此，我们提出了一种更通用的方法，即使用语法进化(GE)以分析形式自动确定开花准备情况[26，27］．在通用电气中，解析函数的形式是通过解码称为的“字”的序列来建立的W整数称为密码子。解码是根据简单的替换规则执行的，该规则在密码子和基本算术运算之间建立了对应关系:“+”，“- - -”，‘*’，' / ',或者表达:X，(X -常量)，1 / (X -常量),在那里X是预言者的名字吗常量是一个常数。

花期的日增量取决于气候因素(14)．

$ ${} \δy (i、t) = \ sum_ {n = 0} ^ {n} \ beta_ f {n} {n} \ cdot (D_{我}(t) Tn_{我}(t) Tx_{我}(t) P_{我}(t) S_{我}(t)) + \ varepsilon_{我}$ $
(14）

在哪里\(β_ {n} \ \; n = 0, \点,n - 1 \)系数,\ \ (f {n}; n = 0, \点,n - 1 \)非线性控制函数和D，Tn，Tx，P，年代气候因素是否组合成一个矢量X（t) = (D我（t)，Tn我（t)，Tx我（t)，P我（t)，年代我（t))。

为了研究来源国对环境的适应，我们将这些国家表示为l=20个二进制变量\ (l = 1, \点,l \)列举了国家:泰国、印度、阿富汗、巴基斯坦、伊朗、菲律宾、巴西、美国、澳大利亚、法国、韩国、土耳其、尼日利亚、越南、伊拉克、荷兰、台湾、墨西哥、肯尼亚。20个样本被标记为“未知”，因为来源国家的信息无法获取，但我们保留了这些样本，因为它们拥有独特的等位基因。对于每一种被列举的植物\ (i = 0 \点,张\)其中的一个l变量\ (d_{我}^ {l} \)接受值“1”表示采集地点，其他值为“0”。控制函数与原产国之间的相互作用在(中加入了附加项。15的加权和形式N·l控制函数的两两乘积Fn和每个二进制站点变量\ (d_{我}^ {l} \)．

然后，模型采用如下形式:

$ ${} \开始{对齐}\δy (i、t) & = \ sum_ {n = 0} ^ {n} \ beta_ f {n} {n} \ cdot (X) + \ sum_ {n = 0} ^ {n} \ sum_ {l = 1} ^ {l} H(左\ \绿色\ zeta_ {l \ cdot n + n} \右\ vert-B_{分钟})\ \ & \四\ cdot \ zeta_ {l \ cdot n + n} \ f {n} (X) cdot \ cdot d ^ {l} _{我}+ \ varepsilon_{我}\{对齐}$ $
(15）

除(中使用的符号外13)和(14)新系数ζl·N+n定义气候控制功能的影响Fn植物表型的地理起源l这条件ζl·N+n≠0分关于植物对原产国环境的适应。为了使新系数的估计更加可靠，我们引入了阈值参数B最小值设所有系数≤B最小值是零。

可用的遗传信息。S2)定义具有不同等位基因组合的样本组。我们表示KSNP和J=3个替代(ALT)和参考(REF)等位基因组合ALT/ALT, ALT/REF和REF/REF分别为0,1和2。然后将GWAS结果包含到我们定义的模型中J·K使同一组的成员在一个SNP位点上有相同的等位基因组合。因此我们定义了一个矩阵D行数等于植物的数量我而且J·K列。然后，矩阵的元素D定义为(16)．因此，通过改变控制函数的权重，回归函数的形式适应于植物的等位基因组合。

$$\begin{array}{@{}rcl@{}} d^{3k+j}_{i} & \，=\，\left\{\begin{array}{ll} 1 & \quad \text{if in plant}\ i \text{SNP} k \text{is}\ j\\ 0 & \quad \text{else}\vspace*{10pt} \end{array}\right。\{数组}$ $
（16）

然后，模型采用如下形式:

$ ${对齐}\ \开始δy (i、t) & = \ sum_ {n = 0} ^ {n} \ beta_ f {n} {n} \ cdot (X) \ \ & \四+ \ sum_ {n = 0} ^ {n} \ sum_ {k = 0} ^ {k - 1} \ sum_ j = {0} ^ {j - 1} H(左\ \绿色\ rho_ {(3 k + j) n + n} \右\ vert-B_{分钟})\ \ & \四\ cdot \ rho_ {(3 k + j) n + n} \ f {n} (X) cdot \ cdot d ^ {3 k + j} _{我}+ \ varepsilon_{我}\{对齐}$ $
(17)

除(中使用的符号外13)和(14),新系数ρ(3k+j）N+n定义基因型-气候因子相互作用的影响。B最小值是系数的阈值参数吗ρ(3k+j）N+n．

未知模型参数的向量θ∈Rr由W密码子,系数\(β_ {n} \ \; n = 0, \点,n - 1 \)，ζl·N+n(或ρ(3k+j）N+n)和阈值参数B最小值和资源数量Y．

在这项工作中，我们实现了一种方法，通过随机最小化模型输出与数据的偏差，自动推断出气候控制函数的解析形式和未知的模型参数，公式(18)和(19)适用于有原产国的型号(15)和基因型(17),分别。

参数的数量r为W= 60码N=5气候控制功能和l=20个原产国r对于包含原产国信息的模型，=172 (15)．模型的参数个数(17),K=10个snp，相同数量的密码子为222个。

数组$ $ \开始{}{@ {}rcl@ {}} Q(\θ)& = & \ sum_ {i = 0} ^{张}(T_{我}-识别\ tau_{我}(\θ))^{2}\ \ & + & \λ\左\ {\ sum_ {n = 0} ^ {n} \左\绿色\ beta_ {n} \右\绿色+ \ sum_ {n = 0} ^ {n} \ sum_ {l = 1} ^ {l} \左\绿色\ zeta_ {l \ cdot n + n} \ \绿色\权利 \} \\ &+&\ α\左\ {\ sum_ {n = 0} ^ {n} \ beta_ {n} ^ {2} + \ sum_ {n = 0} ^ {n} \ sum_ {l = 1} ^ {l} \ zeta_ {l \ cdot n + n} ^{2} \右\}\{数组}$ $
（18)
数组$ $ \开始{}{@ {}rcl@ {}} {} Q(\θ)& = & \ sum_ {i = 0} ^{张}(T_{我}-识别\ tau_{我}(\θ))^{2}\ \ & + & \λ\左\ {\ sum_ {n = 0} ^ {n} \左\绿色\ beta_ {n} \右\绿色+ \ sum_ {n = 0} ^ {n} \ sum_ {k = 0} ^ {k - 1} \ sum_ j = {0} ^ {j - 1} \左\绿色\ rho_ {(3 k + j) n + n} \ \绿色\权利 \} \\ &+&\ α\左\ {\ sum_ {n = 0} ^ {n} \ beta_ {n} ^ {2} + \ sum_ {n = 0} ^ {n} \ sum_ {k = 0} ^ {k - 1} \ sum_ j = {0} ^ {j - 1} \ rho_ {(3 k + j) n + n} ^{2} \右\}\{数组}$ $
(19)

在两个公式中(18)和(19）α= 1,λ正则化参数,τ我（θ)是由一个带有参数的模型预测的从种植到开花的天数θ．

我们使用GE和差分进化完全并行(DEEP)方法的结合[28- - - - - -30.，以拟合模型与可用数据。差别进化由Storn和Price在1995年提出[31作为一种启发式随机优化方法。DEEP由我们开发用于生物信息学领域的应用[28］．它包括最近提出的几项增强建议[29，32］．

估算相互作用和气候因素对模型的影响

由参数向量定义的模型中基因型-环境或原产国-环境相互作用的影响θ以去除感兴趣信息后模型中误差增加的百分比计算(20.)．

$ $ = 100 \ % \ cdot \压裂{\离开(Q(\θ^ {0})- \ sum_ {i = 0} ^{张}(T_{我}-识别\ tau_{我}(\θ))^{2}\右)}{Q(\θ^ {0})}$ $
(20)

在哪里θ0＝θ除了所有ρ∗= 0或ζ∗= 0。

通过对不考虑相关因素的模型和原始模型的预测误差进行比较，估计了气候因子对花期的影响。用Mann-Whitney-Wilcoxon检验比较不同来源国或基因型间气候因子影响平均值的差异。

模型与基因型信息和预测的交叉验证

利用该模型对台湾地区2020-2030年的花期进行了预测。然而，为了预测未来几年的开花时间，我们需要估计模型如何推广到一般的独立数据集，特别是未来的数据集。可用的数据允许我们模拟这样的设置。

首先，使用75%的样本进行训练，25%的样本进行测试，对整个数据集进行4倍交叉验证。其次，为了测试模型在前瞻性数据集中预测开花时间的能力，我们将1984年、1985年和2016年的所有记录(105条)中的20%作为验证集，其余80%作为核心集。

我们使用四次交叉验证来建立一个具有核心集基因型信息的模型。将核心集随机分为包含75%和25%接入的训练集和测试集25次。将模型拟合到训练集，并在测试集上以预测和数据之间开花时间的均方根误差来估计预测的准确性。接下来，选择预测误差最小的最佳模型并在验证集上进行测试，之后用于预测2018年数据(292条记录)的开花时间。交叉验证过程中训练集和测试集开花时间均方误差差异不显著，验证集和2018集开花时间预测精度较高，保证了模型不过度拟合，可以推广到独立的前瞻性数据集。

合成天气一代

我们预测了台湾品种的开花时间。台湾从2020年到2030年的每日天气预报是使用天气生成器程序MarkSim制作的。MarkSim的设计目的是根据每月气候数据的已知来源模拟天气[33- - - - - -37]，并考虑了政府间气候变化专门委员会(IPCC)在2014年第五次评估报告(AR5)中通过的四个代表性二氧化碳浓度分布图(rcp)所描述的社会经济发展情景。根据2100年辐射地球平衡相对于前工业化时期的可能违反值(+2.6、+4.5、+6.0和+8.5)，这些剖面被称为rcp26、rcp45、rcp60和rcp85，对应未来人为温室气体排放可能发生的大范围变化W/米2分别)[38］．

数据和材料的可用性

在当前研究中使用和/或分析的数据集和程序可根据要求从相应作者处获得。世界蔬菜中心绿豆迷你核心收集的条目和表型数据列表可在此访问https://static content.springer.com/esm/art%3a10.1186%2fs12864 - 015 - 1556 - 7/mediaobjects/12864_2015_1556_moesm1_ ESM.xlsx，护照可于http://seed.worldveg.org/search/passport．

改变历史

  • 2021年1月15日

    本文的修订版已经发布，可以通过原文访问。

缩写

APSIM:

农业生产系统模拟器

SNP:

单核苷酸多态性

美国国家航空航天局(NASA):

国家航空航天局

GWAS:

全基因组关联研究

FaST-LMM:

分解光谱变换线性混合模型

主成分分析:

主成分分析

罗斯福:

错误发现率

RCP:

典型的二氧化碳浓度剖面

联合国政府间气候变化专门委员会:

政府间气候变化专门委员会

基于“增大化现实”技术:

评估报告

通用电气:

语法演变

深:

完全平行的差分进化

方差分析:

方差分析

TTF:

开花的时间

参考文献

  1. Dharajiya DT, Ravindrababu Y, Pagi NK。绿豆[Vigna radiata (L，) Wilczek]抗绿豆黄花叶病毒(MYMV)基因型的田间筛选国际微生物学应用科学，2018;7(5): 3472 - 83。

    文章谷歌学者

  2. Vishnyakova MA, Burlyaeva MO, Samsonova MG。绿革兰和黑革兰在俄罗斯联邦的栽培育种前景。Vavilov J Genet Breed. 2018;22日(8):957 - 66。

    文章谷歌学者

  3. Burlyaeva M, Vishnyakova M, Gurkina M, Kozlov K, Lee C-R, Ting C-T, Schafleitner R, Nuzhdin S, Samsonova M, von Wettberg E.绿豆[Vigna radiata] (L，) R. Wilczek]和豇豆[V。曼戈(l)Hepper]在瓦维洛夫研究所(VIR):近100年来育种过程中的性状多样性和趋势。植物资源作物进化。2019。

  4. Schafleitner R, Nair RM, Rathore A，王艳伟，林翠玉，褚淑华，林鹏宇，常建昌，Ebert AW。AVRDC -世界蔬菜中心绿豆(豇豆)核心和迷你核心系列。BMC基因组学,2015;16(1): 344。

    文章谷歌学者

  5. Mondal MMA, Puteh AB, Malek MA, Ismail MR, Rafii MY, Latif MA。绿豆种子产量(豇豆属放射虫纲(L，)威尔切克)与生长和发育方面的关系。科学世界，2012;2012:1-7。

    文章谷歌学者

  6. 王晓燕，王晓燕，王晓燕，等。国际绿豆试验的基因型和环境变异分析。Euphytica。1981;30(2): 301 - 11所示。

    文章谷歌学者

  7. 史温德尔，波尔曼，JM。光周期反应(vigna radiata [l，] wilczek)~的遗传。Euphytica。1978;27:325-33。

    文章谷歌学者

  8. Ellis RH, Lawn RJ, Summerfield RJ, Qi A, Roberts EH, Chay PM, Brouwer JB, Rose JL, Yeates SJ, Sandover s对六种一年生作物开花时间的可靠预测，4 .栽培和野生绿豆。Exp阿格利司。1994;(1): 30 31-43。

    文章谷歌学者

  9. 绿豆基因型x环境互作及稳定性分析。国际农业兽医学报，2013;5(1): 62 - 70。

    文章谷歌学者

  10. Godwin ID, Rutkoski J, Varshney RK, Hickey LT.植物育种的技术前景。应用理论。2019;132(3): 555 - 7。

    文章谷歌学者

  11. 王晓燕，王晓燕，王晓燕。基因组工具在绿豆[Vigna radiata (L，) Wilczek]改良中的作用。Legum Res Int J. 2017。

  12. 金sk, Nair RM, Lee J, Lee S-H。用于未来育种计划的绿豆基因组资源。植物科学进展2015;6.

  13. Kang YJ, Kim SK, Kim MY, Lestari P, Kim KH, Ha B-K, Jun TH, Hwang WJ, Lee T, Lee J, Shim S, Yoon MY, Jang YE, Han KS, Taeprayoon P, Yoon N, Somta P, Tanya P, Kim KS, Gwag J- g, Moon J- k, Lee Y-H, Park B-S, Bombarely A, Doyle JJ, Jackson SA, Schafleitner R, Srinives P, Varshney RK, Lee S- h。绿豆的基因组序列和维尼亚属植物的进化。Nat Commun。2014;5(1): 5443。

    中科院文章谷歌学者

  14. 杨建军，张志刚，张志刚。作物模型的应用与局限性。阿格龙j . 1996;88:704-16。

    文章谷歌学者

  15. Mabhaudhi T, Chibarabada TP, Chimonyo VGP, Modi AT。模拟气候变化的影响:班巴拉花生(Vigna underground)的案例。物理化学家地球零件A/B/C。2018;105:25-31。

    文章谷歌学者

  16. 查普曼高级律师，库珀M，哈默GL，巴特勒DG。环境互作对高粱基因型的影响。不同季节干旱胁迫的发生频率与杂交产量的位置效应有关。德国农业公司2000;51(2): 209。

    文章谷歌学者

  17. 乔汉YS, Douglas C, Rachaputi RCN, Agius P, Martin W, Skerman .绿豆生理特性及绿豆作物模型的建立。:程序。黄金海岸:2010。11页。

  18. Hwang C, Correll MJ, Gezan SA, Zhang L, Bhakta MS, Vallejos CE, Boote KJ, Clavijo-Michelangeli JA, Jones JW。下一代作物模型:模拟普通豆类早期营养和生殖发育的模块化方法(菜豆寻常的L). agrosyst . 2017;155:225-39。

    中科院文章谷歌学者

  19. 满足全球粮食需求:通过遗传x环境x管理交互实现潜力。阿格龙j . 2015;107:1215-26。

    文章谷歌学者

  20. 植物非生物胁迫耐受性的解剖与建模。植物生物学，2010;13:206-12。

    文章谷歌学者

  21. 当地适应的概念问题。生态。2004;7(12): 1225 - 41。

    文章谷歌学者

  22. Lasky JR, Upadhyaya HD, Ramu P, Deshpande S, Hash CT, Bonnette J, Juenger TE, Hyma K, Acharya C, Mitchell SE, Buckler ES, Brenton Z, Kresovich S, Morris GP。高粱地方品种的基因组环境关联可以预测适应性性状。Sci放置2015;1(6)。http://arxiv.org/abs/http: / / advances.sciencemag.org/content/1/6/e1400218.full.pdf。

  23. 李佩特，李士杰，刘勇，Kadie CM, Davidson RI, Heckerman D.全基因组关联研究的FaST线性混合模型。Nat方法。2011;8(10): 833 - 5。

    中科院文章谷歌学者

  24. 层JD。阳性错误发现率:贝叶斯解释和问价值。统计年鉴》2003年;31日(6):2013 - 35。

    文章谷歌学者

  25. 斯塔克豪斯PW，佩雷斯R，森古普塔M，纳普K，米科维茨JC，施莱默J，斯卡里诺B，张T，考克斯SJ。用于10-100公里长期全球太阳能资源开发的新卫星数据产品评估。见:太阳能2016年会议论文集。旧金山:国际太阳能协会:2016年。1 - 6页。

    谷歌学者

  26. 奥尼尔M，瑞安C.语法进化。IEEE跨进化计算。2001;5(4): 349 - 58。

    文章谷歌学者

  27. Noorian F, de Silva AM, Leong PHW。gramEvol英语的语法进化R．J Stat soft . 2016;71(1): 1-26。

    文章谷歌学者

  28. 基因调控网络的DEEP -差分进化完全并行方法。J Supercomput。2011;57:172-8。

    文章谷歌学者

  29. 科兹洛夫K, Samsonov AM, Samsonova M.差分进化完全并行法参数优化软件。PeerJ computational science . 2016;2:74。

    文章谷歌学者

  30. 科兹洛夫KN，诺维科娃LY，塞弗洛娃IV, Samsonova MG。大豆生长发育依赖气候因子的数学模型。Biofizika。2018;63(1): 175 - 6。

    谷歌学者

  31. 差分进化——连续空间上全局优化的一个简单而有效的启发式。技术报告TR-95-012, ICSI。1995.

  32. 通过控制种群多样性来适应差异进化的参数。第四届科学计算的符号和数值算法国际研讨会，数学信息学系列，XL卷。Timisoara: Analele Universitatii Timisoara: 2002。p . 385 - 97。

    谷歌学者

  33. Srinivasa Rao M, Swathi P, Rama Rao CA, Rao KV, Raju BMK, Srinivas K, Manimanjari D, Maheswari M.未来气候变化情景下花生斜纹夜蛾预测代数的模型和情景变化。PLoS ONE。2015;10(2): 0116762。

    文章谷歌学者

  34. 王晓峰，王晓峰。基于三阶马尔可夫模型的降水时空变化。1997;86(2): 127 - 38。

    文章谷歌学者

  35. 对插值的气候面拟合三阶马尔可夫降雨模型。农林气象，1999;97(3): 213 - 31所示。

    文章谷歌学者

  36. MarkSim:生成拉丁美洲和非洲每日天气数据的软件。阿格龙j . 2000;92:9。

    文章谷歌学者

  37. Jones PG, Jones AL，国际热带农业中心。MarkSim:为作物建模和风险评估生成模拟天气数据的计算机工具。国际热带农业中心。OCLC: 54981281。2002.

  38. van Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, Hibbard K, Hurtt GC, Kram T, Krey V, Lamarque J- f, Masui T, Meinshausen M, Nakicenovic N, Smith SJ, Rose SK。这张。2011;109(1 - 2): 5-31。

    文章谷歌学者

  39. Abebe TD, Naz AA, Léon J.景观基因组学揭示大麦(Hordeum vulare L.)的局部适应性特征植物科学进展2015;6.

  40. De Kort H, Vandepitte K, Bruun HH, closett - kopp D, Honnay O, Mergeay J.景观基因组学和一个普通的花园试验揭示了欧洲各地树种对温度的适应性分化赤杨皮需．摩尔生态。2014;23日(19):4709 - 21所示。

    中科院文章谷歌学者

  41. 朱科洛A，金枪鱼M，吉安弗兰切斯基L, Pè M.单子叶植物模式短尾草的环境适应:一种多层面的方法。BMC基因组学,2014;15(1): 801。

    文章谷歌学者

  42. 韦斯滕根OT，伯格公关，肯特议员，布里斯汀AK。通过调查与全球育种和地方品种组相关的SNP多样性揭示非洲玉米的空间结构和气候适应。PLoS ONE。2012;7(10): 47832。

    文章谷歌学者

下载参考

确认

我们感谢Svetlana Surkova, Vitaly Gursky和Margarita Vishnyakova的有益讨论。这项工作是利用彼得大帝圣彼得堡理工大学超级计算机中心的计算资源完成的。http://www.scc.spbstu.ru)．

关于这个补充

本文已发布的一部分BMC植物生物学2020年增刊第20卷第1期:第五届国际科学会议“植物遗传学、基因组学、生物信息学和生物技术”(PlantGen2019)的文章选集．该补刊的全部内容可在网上查阅//www.cinefiend.com/articles/supplements/volume-20-supplement-1．

资金

这项工作得到了RScF #18-46-08001号拨款的支持(研究的设计、模型开发和交叉验证、开花时间预测、数据分析和解释以及撰写手稿)。《娱乐周刊》还得到了美国农业部通过佛蒙特州实验站提供的Hatch基金的支持。CRL和CTT得到台湾科技部107-2923-B-002-004-MY3的支持。本文的发表得到了RScF #18-46-08001拨款的支持。表型和基因型数据的收集得到了澳大利亚国际农业研究中心(acar)资助的国际绿豆改良网络(ci -2014-079)和世界蔬菜中心的其他核心捐助者:中华民国(台湾)、美国国际开发署(USAID)、澳大利亚国际农业研究中心(acar)、泰国、菲律宾、韩国和日本的资助。

作者信息

从属关系

  1. 彼得大帝圣彼得堡理工大学，29 Polytechnicheskaya，圣彼得堡，195251，俄罗斯

    Konstantin Kozlov, Alena Sokolkova和Maria Samsonova

  2. 国立台湾大学，台北，台湾

    李成瑞、丁卓逖

  3. 台湾台南世界蔬菜中心

    罗兰Schafleitner

  4. 佛蒙特大学植物与土壤科学系，美国佛蒙特州伯灵顿市卡里根路63号，邮编05405

    Eric Bishop-von Wettberg

  5. 分子与计算生物学项目，加州大学帕克分校，洛杉矶，加利福尼亚州，24105

    谢尔盖Nuzhdin

作者
  1. 康斯坦丁·科兹洛夫
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  2. 阿勒娜Sokolkova
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  3. Cheng-Ruei李
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  4. Chau-Ti Ting
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  5. 罗兰Schafleitner
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  6. Eric Bishop-von Wettberg
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  7. 谢尔盖Nuzhdin
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

  8. 玛丽亚Samsonova
    看来作者出版物

    您也可以在中搜索这个作者PubMed谷歌学者

贡献

SN, MS, EW和KK构思和设计了这项研究。CRL、CTT和RS准备了数据集。AS进行GWAS分析。KK, SN和MS建立了模型。KK进行了计算。KK、SN、RS和MS对结果进行了分析。AS、KK、SN、EW、RS和MS编写了本文。所有作者阅读并批准了最终稿件。

相应的作者

对应到玛丽亚Samsonova．

道德声明

伦理批准和同意参与

不适用。

同意出版

不适用。

相互竞争的利益

作者声明他们没有竞争利益。

额外的信息

出版商的注意

施普林格自然对出版的地图和机构附属的管辖权要求保持中立。

本文已更新。原始出版物包含不正确的历史日期。

补充信息

额外的文件1

支持信息。附加文件1包含基于SNP的群体的信息，这些群体的气候数据，语法进化方法的细节。

权利和权限

，在2020年出版。开放获取本文遵循创作共用署名4.0国际许可协议(Creative Commons Attribution 4.0 International License)，该协议允许在任何媒体或格式中使用、分享、改编、分发和复制，只要您给予原作者和来源适当的署名，提供创作共用许可协议的链接，并说明是否有更改。本文中的图片或其他第三方材料包含在文章的创作共用许可中，除非在材料的信用额度中另有说明。如果材料不包含在文章的创作共用许可中，并且您的预期用途不被法律法规允许或超出了允许的用途，您将需要直接从版权所有者那里获得许可。欲查看此许可证的副本，请访问http://creativecommons.org/licenses/by/4.0/．创作共用公共领域奉献放弃书(http://creativecommons.org/publicdomain/zero/1.0/)适用于本文提供的数据，除非在数据的信用额度中另有说明。

再版和权限

关于这篇文章

通过CrossMark验证货币和真实性

引用这篇文章

K.科兹洛夫，A.索科尔科娃，李，CR。et al。豇豆开花时间的动态气候模型。BMC植物杂志20.202(2020)。https://doi.org/10.1186/s12870-020-02408-1

下载引用

  • 收到了：

  • 接受：

  • 发表：

  • DOI：https://doi.org/10.1186/s12870-020-02408-1

关键字

  • 豇豆属
  • 绿豆
  • 模型
  • 气候因素
  • GWAS

BMC植物生物学

ISSN: 1471 - 2229

联系我们